COLUMBIA 查询优化器如何提升性能(上)
ABSTRACT
COLUMBIA 项目聚焦于效率:如何在不损害拓展性的前提下,使设计实现的 Columbia Query Optimizer 获得巨大的性能提升。
本项目是基于 Cascades Optimizer Framework 的 Top-Down 优化算法,并通过重构搜索空间和搜索算法来简化 Top-Down 优化器设计:通过实现两种裁剪技术(pruning techniques)取得了极大的性能提升。此外,通过增加友好的用户接口和广泛的跟踪支持(extensive tracing support)来提升本项目的可用性。
1. Introduction
尽管查询优化(query optimization)成为研究项目已经超过15年,但是 query optimizers 仍是关系数据库中最大最复杂模型之一,这使得他们的开发和变动成为困难且耗时的任务。随着现代数据库的需要发展,这一情形会变得更加复杂,因此催生了新的技术。
在过去的几年里,也开发了几代商业和研究性质的优化器,在拓展性和效率做出提升:
- 第一代致力于可拓展的优化器技术,认识到在新数据模型(new data models)、查询类别(query class)、语言和评估技术(evaluation techniques)等方面存在需求。因此诞生了一些列项目,诸如 Exodus、Starburst,他们的目标是使优化器更加模块化,更易于拓展。他们使用到的技术包括 layering of components、基于规则的转化等。这些成果存在一些短处,比如增加拓展的复杂度、搜索性能以及更加偏向于于面向记录的数据模型(record-oriented data module)
- 第二代可拓展的优化器,诸如 Volcano optimizer generator,增加了更加复杂的搜索技术,更多地使用了物理属性来指导搜索以及更好地控制搜索策略来实现更好的搜索性能。虽然这些优化器在一定程度上更加灵活了,但是仍难以拓展
- 第三代优化器,诸如 Cascades、OPT++, EROC 和 METU,开始使用面向对象技术(object-oriented design)来简化实现、拓展和更改优化器,与之同时保持效率并且是的搜索策略更为灵活。这最新一代的优化器已经达到的复杂程度,已可以满足现代商业数据库系统的要求。这一点可以从他们的工业实现(Cascades by Microsoft and Tandem, EROC by NCR)也可以看出。
按照搜索策略划分,这三代查询优化器可以被归位两类:
- Starburst style: bottom-up dynamic programming optimizers
- Cascades style: top-down branch and bound rule-driven cost based optimizers
bottom-up 优化算法当前广泛用于传统商业数据库系统中,因为至少在传统应用中被认为是有效的。但是由于 bottom-up 算法要求将原始问题分解为子问题,使其相比较 Top-down 算法,bottom-up 优化算法与生俱来就缺乏可拓展性。此外,为了在大查询中实现可以接受的性能,bottom-up 类算法中必须要用启发式(heuristics)策略。
尽管在此之前的 top-down 优化器实现已表明此类优化器难以实现和 DownTop相匹敌的性能,但是本论文认为 top-down 优化器在效率上和拓展能力一样有优势。因此为论证这一观点,本论文的剩余部分就是描述我们如何设计另一个 top-down 优化器: Columbia
Columbia 优化器在 Cascades Optimizer Framework 的基础上,广泛利用 C++ 面向对象的特性以及细心的工程师,来啊简化 top-down 算法,进而维持 top-down 拓展性的同时实现提升性能的目的,本论文算法只定义了少量关键的带有虚函数的抽象基类,根据这些基类来完整实现搜索策略。这些搜索策略调用这些基类的虚函数来执行具体地搜索,并基于成本(cost-based)对搜索空间进行裁剪。
因此,从这些抽象基类派生新的子类并重写基类虚函数,就可以轻松拓展优化器来操作其他的复杂数据模型、添加新的 operators 和转化规则。故而本文聚焦于关系数据模型中的优化,不再讨论优化器的拓展性。
为了,减少 CPU 和 Memory 的使用率,本论文的 Columbia 框架会使用几个工程技术来提升效率,诸如:
- 一个快速的 hash function 来消除重复的表达式;
- 一个 group exepression 中 logical expressions 和 physical expressions 的分离
- 小而紧凑的数据结构
- 有效的算法来优化分组和输入
- efficient way to handle enforcers (that is what
Columbia 优化器提供了两个重要的技术:
group pruning:这个技术这极大地裁剪了搜索空间,并且毫不损害生成的执行计划。在低层次(low-level)物理计划生成前,优化器会先计算高层次(high-level)物理计划的代价(cost),这些提前计算的代价用于后续优化代价上限,本文后面将会展示在很多场景下,这些上限可以避免生成整个 group expressions,进而裁剪搜索空间中大量可能的查询计划。
global epsilon pruning:这个技术通过生成可以接受的次优方案(close-to-optimal solutions)来裁剪搜索空间。当一个solution足够接近最优方案,那么这个优化目标就算完成了,进而许多其他的路径就可以忽略。
2. Terminology
本章主要回顾查询优化文献中的术语和基本概念,这些也将用于描述 Columbia 框架的设计和实现。
2.1. Query Optimization
查询处理的目的是从 DML 提取出表达式,并基于数据库的数据进行评估。
图1 展示了查询处理的步骤,
- DML 语句中的原始查询被解析成代数上的逻辑表达式树(logical expression tree),
- 接着这逻辑表达式树传递给查询优化器,将逻辑查询转换为物理计划:物理执行计划就可以在真正持有数据的数据结构上执行
这个过程会执行两种转化:
Logical transformations:创建查询可能的逻辑形式(logical forms)
physical transformations:选择一个特别的物理算法来实现一个逻辑算子(logical operator),比如使用 sort-merge join 来实现 logical join
通常,这个过程会生成大量的执行计划来实现逻辑查询树,因此需要查询优化器主要关注的就是如何找到最优的执行计划,即代价最低的路径。只要选中一个最优物理计划,就会被传递给查询执行引擎(query execution engine)。查询执行引擎使用有序数据作为输入来执行物理计划,得到的查询到结果即整个输出。
如果我们只关注用户层,那么查询处理过程就被隐藏在查询处理器的黑盒之中。用户提交SQL请求时,希望系统正确又快速输出结果。正确性(Correctness)是查询处理器的基本要求,而性能(performance)是查询处理器所需要的特性和主要关注点。从查询处理的系统层次看,查询优化器在数据库系统的高性能至关重要。
生成的物理计划中,包含了大量能完成正确性的执行计划,但是具有迥异的执行性能(execution performance),优化器的目标之一就是发现最佳执行性能的物理计划。一个朴素的方法就是生成所有可能的路径,然后遍历选择代价最低的路径。但是,遍历所有可能的路径的代价是极其高的,因此即便是非常简单的查询语句都会生成大量的路径,因此优化器必须以某种方式缩小搜索空间。
查询优化是个复杂的搜索问题,研究表名这个问题的简单版本就是NP-hard。一个搜索策略对于优化器成功与否至关重要。
2.2. Logical Operators and Query Tree
逻辑算子 Logical operators 属于高级(high level)算子,仅表征了数据转换关系,并不指定使用哪种具体的物理执行算法。在关系数据模型中,Logical operators 接受多个表作为输入,并产生单表输出。每个 logical operator 接受固定数量的输入(输入的数量叫做 arity),并有多个用于区分 operators 变体的参数。
有两个经典的 logical operators:
- GET Operator:即Scan操作,他没有输入的table,并且有一个表名参数。GET Operator 从磁盘中获取数据,并输出给后续的Operators
- EQJOIN Operator:有两个输入table,即进行JOIN操作的左表、右表,输入的参数包含着和左表、右表相关的predicates。
查询树(query tree) 是 query 的树形结构表征方式,并被用于优化器的输入。一般地,查询树会被表征为 logical operators 的树形结构,每个 TreeNode 都是一个 logical operator,有零个或者多个 logical operators 作为输入,这个 TreeNode 的子节点数量等于输入的 logical operators 的数量,也即 arity。这个查询树的叶结点即 arity = 0 的 operators(比如 GET Operator)。
图-2 是个查询的树形表征的例子。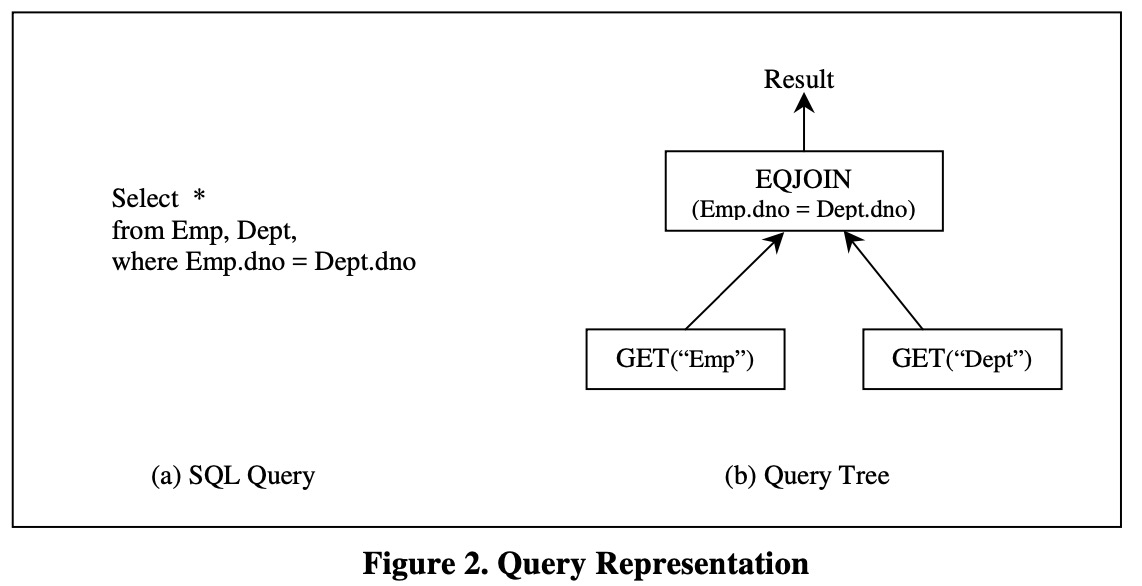
query trees 用于指定执行 operators 的顺序,比如为了执行查询树上的 top operator,那他的输入就必须先执行。在图-2的例子中 EQJOIN operator 的两个输入,接受的就是两个 GET operators 的输出。而 EQJOIN 的输入参数,即 Emp.dno=Dept.dno,描述的就是 JOIN 的条件。而这个 EQJOIN 的输出即整个查询所需的结果。GET operators 没有输入,因此他们就是叶节点,用于产生本次查询评估所需的数据源,而 GET operator 的输入参数表征的是所需读取表的表名,比如 Empt、Dept。
2.3. Physical Operators and Execution Plan
Physical operators 表征的实现特定数据操作的具体算法。在数据库中,对于一个 logical operators,通常存在一个或者多个 physical operators 实现。
- EQJOIN logical operator 可以使用 nested-loops、sort-merge join 或者其他算法来啊实现,而具体的算法也可以使用不同的 physical operator来实现,比如 nested-loops 一般是用 LOOP-JOIN physical operator实现,而 sort-merge 算法一般是用 MERGE-JOIN physical operator实现。
- GET logical operator 的经典实现算法是按照表的存储顺序进行 scan,一般是使用 FILE_SCAN physcail operator。
将查询树中的 logical operators 替换为 physical operators 就产生了一棵 physical operators 树,一般叫做执行计划(Execution Plan)。图-3 展示了由图-2查询计划生成的两个执行计划。
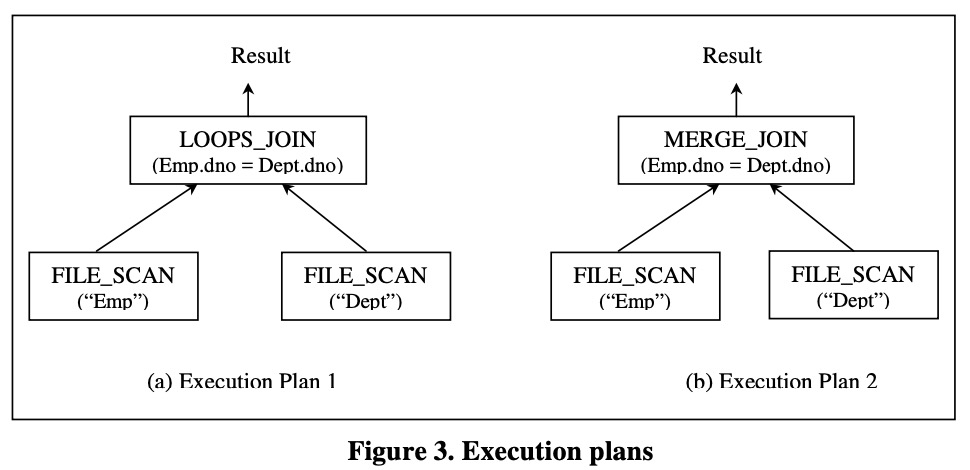
执行计划具体说明了如何评估查询(evaluate the query):每个执行计划都有一个执行成本,对应着 cost model 和catalog infomation。对于一个指定查询,优化器生成的最优执行计划会作为查询执行引擎的输入,执行引擎会基于数据库系统中的数据执行整个算法来产生本次查询的输出结果。
2.4. Groups
给定的查询可以由另一个在逻辑上等价的查询树来表征:如果两个查询树在任何主流的数据库上的输出都完全相同,则他们是 逻辑上等价的。通常,每一个查询树都有一个或者多个执行计划来实现查询树并产生完全相同的结果,那么这些执行计划就是逻辑上等价的。
图-4 展示了几个逻辑等价的查询树以及实现这些查询树产生逻辑等价的执行计划。

如图-4所示,我们使用 $\Join$ 符号来表征 EQJOIN operator,$\Join_L$ 表征 LOOPS_JOIN operator,$\Join_M$ 表征 MERGE_JOIN。出于简洁的目的,使用参数表征 GET,加上下标F表征 FILE_SCAN,比如图-4中使用 $C$ 表征 GET(“C”),用 $C_F$ 表征 FILE_SCAN(“C”)。
图4(a) 和 图4(b) 是两个逻辑等价的查询树,差别只在于 logical operator 的顺序;(a-i) 个 (a-ii)是两个逻辑等价的执行计划,他们的区别在于使用不同的JOIN算法。
那么我就可以使用 expressions 来表征查询树和执行计划(以及他们的子节点):一个 expression 由一个 operator 和它的零个或者多个输入组成,根据 operator 的类型这个 expression 也被区分为 logical expression 和 physical expression,因此查询树即 logical expressions,执行计划即 physcical expressions。
考虑到一个 logical expression 就存在大量逻辑等价的 logical expressions 以及生成的 physical expressions,如果将他们都放入到一个 group 中并定义他们的共同特征(common characteristics)就变得非常有用。
Group 是一组逻辑等价的 exprssions 集合。一般地,一个 group 包含所有逻辑等价的 logical expressions,以及基于他们生成的逻辑等价的 physical expressions。显然,group 中的每个 logical expression 对应的 physical expressions 不止一个。图-5展示的 group 包含了图-4中表达式的以及其他的等价表达式,

我们通常用其中一个 logical expressions 来表示一个 group,比如 $(A \Join B) \Join C$,或直接使用 $[ABC]$。图-5 中展示了 $[ABC]$ group 中所有等价的逻辑表达式及部分物理表达式。从图-5中可以看到,即便是逻辑表达式也存在大量等价的表达形式。
为了减少 group 中表达式的数量,引入 Multi-Expressions。一个 Multi-Expressions 有一个 logical/physical operator,并将 groups 作为输入。 multi-expression 和 expression 不同点在于输入: 前者以 groups 作为输入,后者以其他 expressions 作为输入。比如 Multi-expression $[A \Join B] \Join [C]$ 表示 EQJOIN operator 的输入是 $[A \Join B]$ 和 $[C]$ 两个 group。由于在一个 group 中鲜有等价的 multi-expression,因此能极大得节省搜索空间。
图-6 展示了 group [ABC] 中等价的 Multi-Expressions,相比较图-5 中 Expression 的数量更少。 也就说通过使用 Multi-Expressions,就可以将 group 重新定义为一系列等价 Multi-Expressions 的集合。

在查询的通用处理过程中,在生成最终结果前会先产生许多中间结果,即许多tuples的集合。而中间结果就是通过计算一个 group 对应的执行计划得到的。换言之,group 就对应着中间结果,而这些groups被叫为 intermediate groups,而生成最终结果的group,就叫做 final group。
The Logical properties of a group are defined as the logical properties of the result, regardless of how the result is physically computed and organized. These properties include the cardinality (number of tuples), the schema, and other properties. Logical properties apply to all expressions in a group
logical properties
一个group中的所有expressions共享一个 logical properties,它被定义为这个group输出结果的逻辑属性,而不在乎结果实际上的计算、组织方式。 logical properties 包括:
- cardinality: tuples 的数量,即行数
- schema
- 其他属性
2.5. The Search Space
search space 表示给定初始查询的逻辑查询树和物理计划。为了节省搜索空间,将 search space 表征为 group 集合,每个 group 都将其他 groups 作为输入,而最上层的 group 也就是 final group(root group),它对应着初始查询的最终结果。 图-7 展示了一个查询的初始搜索空间(initial search space)。

在 initial search space 中,每个 group 仅包含一个源自于 initial query tree 的 logical expression。
也就是说,在生成初始搜索空间后,每个 group 需要基于已有的 logical expression 生成逻辑等价的新表达式。
在图-7 中,最上层的 group $[ABC]$ 就是该查询的最终输出,即 final group,它就是图-7中三个 join 的最终结果。
我们可以从一个 initial search space 获得一个 initial query tree。query tree 上的每个节点(node)都对应着搜索空间中每个 group 的 Multi-expression 上的 operator。
比如,fig-7 中有 final group $[ABC]$ ,它由 $EQJOIN$ operator 和 $[AB], [C]$ 两个输入 groups 组成。我们可以获得这么一个 query tree:以 EQJOIN 作为最上层的 operator,输入的 Operator 源于 $[AB], [C]$ 两个 groups,然后分别递归 $[AB], [C]$ 两个 groups 直到遇到没有输入的groups,即叶子组。
从 initial search space 派生出来的 query tree 就刚好是 initial query tree。换言之,initial search space 表征了 initial query tree。
在优化的过程中, 每个 group 会生成大量逻辑上等价的 logical expressions 和 physical expressions,进而导致搜索空间急剧膨胀。与此同时,在生成 physical expressions 的过程中,这些 physical expressions 的执行代价( execution costs)也都会被计算出来。在某种意义上,生成所有的 physical expressions 就是优化器的目标,然后从中找到代价最低的 physical expression即可。但是为了生成所有 physical expressions,就必须先构造出所有的 logical expressions,这是因为physical expression 只是 logical expression 的一种实现。
一个完全被膨胀的搜索空间被叫作 final search space,即表示了一个查询的所有逻辑上等价的 expressions。
实际上,使用递归的方式可以从 final search space 获得所有可能的 query tree 和 exec plan,就像使用递归方式从 initial serach space 获得 initial query tree。 在搜索空间中,每个 Multi-expressions 上的 operator 对应着着 query tree 上的一个 operator node 或者一个执行计划。
由于搜索空间中的一个 group 就包含了大量逻辑上等价的表达式,那么 final search space 也会呈现了大量的 query trees 和 execution plans。
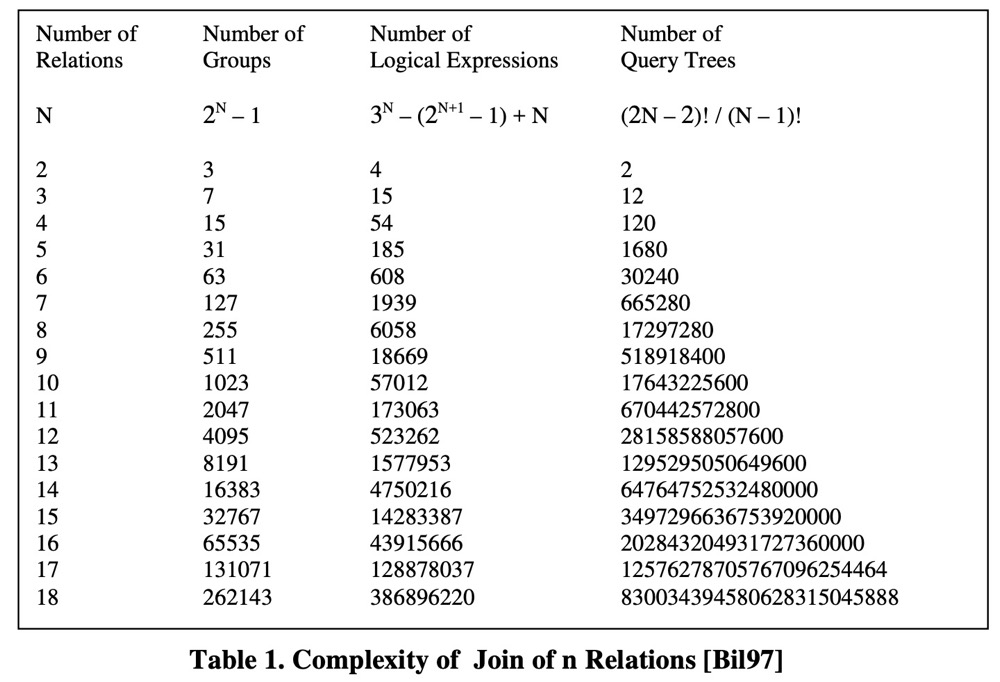
表-1 显示了由 N 个表 JOIN 得到的完整逻辑搜索空间(仅显示了 logical expressions 的数量)。比如, 4 个表进行 JOIN 的逻辑搜索空间就有15个 groups,包含了 54 个 logical expressions,呈现了120个query trees。
从表-1可以看出,即便只考虑 logical expressions,搜索空间的大小也会随着 JOIN 的表增多而呈现指数趋势增长。而 logical expressions 的数量取决于 logical operator 有多少种算法实现。比如当前搜索空间中有 N 个 logical expressions,并且数据库系统支持 M (M >= 1) 种 join 算法实现,那么搜索空间就将会有 $M * N$ 个 logical expressions,也就说 physical expressions 的数量不会少于 logical expressions 的数量。
2.6. Rules
rule 描述得是如何将一个表达式转化为一个在逻辑上等价的新表达式。因此,许多优化器会通过使用 rules 来对一个 initial query 生成一系列逻辑上等价的表达式,达到扩充 initial search space 的目的。
每个 rule 都会被定义为一个pair:
- pattern: 定义的是输入的 logical expressions 的结构,即什么样的输入表达式可以应用这条 rule(注意: rule 仅能用应用于 logical expressions),
- subsitute: 定义的是输入表达式在应用这条规则之后,输出结果的结构
当扩充搜索空间时,优化器会审视每个 logical expression 并检查 rules set 中是否存在 rule 的 pattern 能与该表达式相匹配。如果存在,则会根据 rule 中 substitute 定义的输出表达式结构,应用这条规则来生成新的逻辑上等价的表达式。
Cascades 使用表达式来表示 pattern 和 substitues: 其中 pattern 总是 logical expressions,而 subsitutes 即可以是 logical expressions 也可以是 physical expressions。
rules 的两种通用类型是:
- Transformation rules: 当 substitute 是 logical expression 时, rule 被叫做 transformation rules。
- implementation rules: 当 substitute 是 physical expression 时, rule 被叫做 implementation rules。
如图-8,$EQJOIN_LTOR$ 就是一种 transformation rule,$EQJOIN_MERGEJOIN$ 就是一种 implementation rules。