Radix-Join Cluster Algorithm

现在很多 JOIN 算法在进行 JOIN 操作之前，会先将输入划分成多个 clusters/partitions，再在每个 cluster 内部进行 JOIN，以便使用多线程等来加速 JOIN。现在主流的分区算法大都是基于 radix-cluster algorithm[1] 及其衍生对输入进行分区。

现在的 join 算法为提高性能，基本都是想着如何充分发挥硬件的特性，比如线程，NUMA 内存分配特性，SIMD，TLB entries、cache lines等。

本文只是作为后续 JOIN 算法的一个铺垫，因此主要介绍 radix-cluster algorithm 本身，其他部分可参考原文[1]。

PARTITIONED HASH-JOIN

Shatdal et al.[2] 提出了一种在 main-memory 下 Grace Join 算法的变体。

该算法先基于一个 hash-number 将两个输入划分都分别为 H 个不同的 clusters，使得每个分区都能纳入 memory cache，这种方式比常规基于 bucket-chained hash join 性能更好。该算法简单明了，直接使用了一个分簇算法(clustering-algorithm)： 只扫描输入一次，并将每个被扫描的 tuple 插入到输出中一个 cluster

如图-8所示，将左侧的输入随机的划分到 H 个单独的 cluster 中。

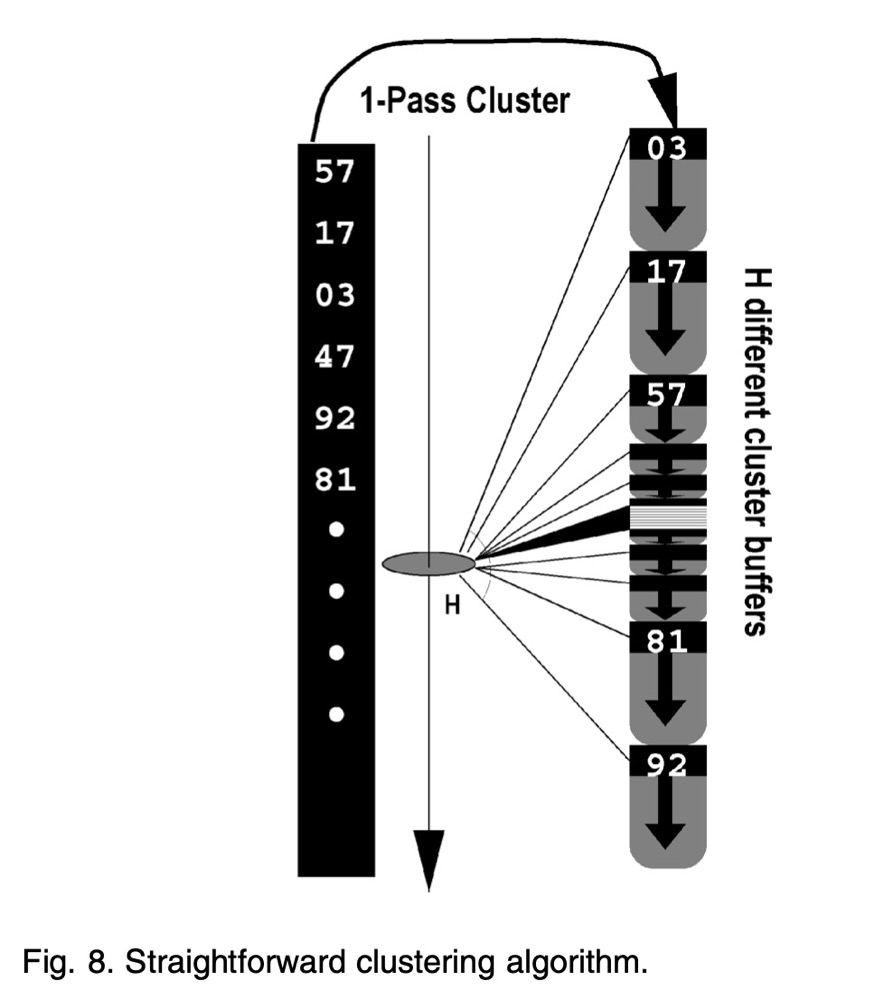
radix-join-1

这个算法，问题就出在随机上，因为会破坏内存访问的局部性，这点从图-8可以看出，输出的H个 clusters 和输入分布基本没啥关系。而且由于需要把每个 cluster 都尽可能纳入 memory-cache 中，就需要 H 尽可能大，使得产生的每个 cluster 就会尽可能小才能一次性纳入cpu cache。那么当 H 非常大时，又有两个因素会导致性能退化：

  • 如果 H 超过 TLB entries 的数量，那么每次访问内存（memory reference）都会产生一次 TLB miss；
  • 如果 H 超过了 L1 or L2 可用的 cache lines 数量，cache thrashing 现象就会出现，进而导致 cache miss 次数激增。

为解决这两个问题，提出了 Radix-Cluster Algorithm ，使得即便H非常大，也具有非常低的随机访问，进而提高性能。

Radix-Cluster Algorithm

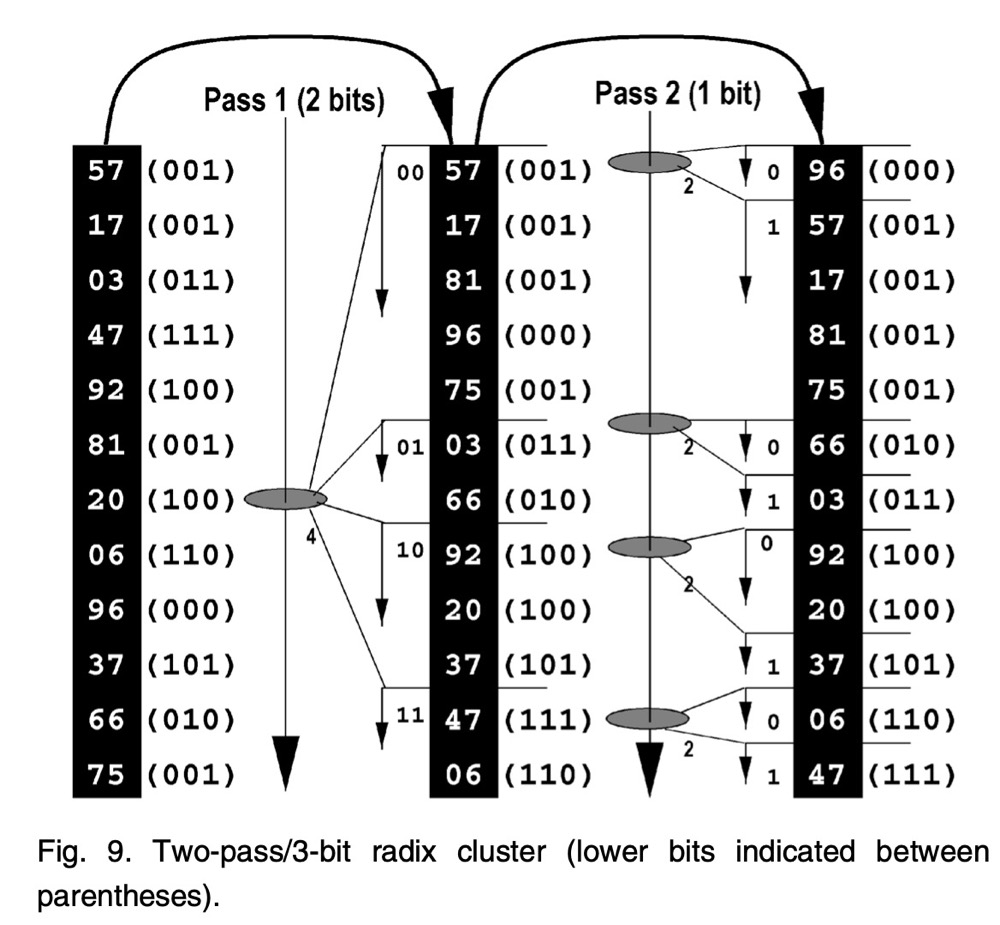
如图 9 所示，radix-cluster algorithm 使用多个阶段（论文中叫 pass）将输入划分为 H 个 clusters，

radix-join-2

下面会先阐述下算法，然后以图-9为例进行说明算法。

radix-clustering 算法是基于某列生成的整数 hash value 的低 $B$ bits 上实现的：
该算法有连续的 P 个 pass ，每个 pass 都基于输入 tuple 的 $B_p$ 个 bits 对输入进行分区，且该 $B_p$ 个 bits 的位置是从最左侧开始计算的 $\sum_1^pB_p$ bits。

比如图-9中 $B = 3$，其中 $P=2$，$B_1 = 2$，$B_2=1$：

  • 第一个 pass 先使用 $B_1$ bits，目前总共使用的是从最左侧开始计算的 $2=\sum^{p=1}_1B_p$ 个 bits 进行对一个 pass 输入进行分区；
  • 第二个 pass 再使用 $B_2$ bits，目前总共使用的是从最左侧开始计算的 $3=\sum^{p=2}_1B_p$ 个 bits 对第二个 pass 输入进行分区

第二个 pass 是在第一个 pass 的基础上再进行分区，因此看似只使用了一个 bit，实际上包含了第一个 pass 中两个bits的影响，因此说第二个 pass 使用从最左侧开始的 3 个 bits也没问题。

radix-cluster 算法创建的 clusters 数量 $H = \prod^p_1 H_p$，其中后一个 pass 会基于上一个 pass 输出的每个 cluster 继续子划分为 $H_p = 2^{B_p}$ 个新的 cluster。

因此当算法开始时，整个输入就被视为一个完整的 cluster，第一个 pass 就被划分为 $H_1 = 2^{B_1}$ 个新的 clusters，然后在下一个 pass 继续基于 $H_1$ 个 clusters 再次划分，每个 cluster 又产生 $H_2 = 2^{B_2}$ 个新的 clusters，因此两个 pass 就一共产生了 $H_1 * H_2$ 个 clusters。

特别地，当 $P = 1$ 时，radix-cluster 算法即类似上述简单明了的划分算法。

  • 为什么说 radix-cluster 算法在 H 很大时局部性更好？这个观察图-9两个pass的输出应该能得出结论。
  • 此外，为便于演示，在图-9所示的整数值表中没有使用哈希函数。然而，在实际中，即便是整数值，最好也使用一个hash函数，来确保值的所有位数都能发挥作用。

radix-cluster 算法有诸多好处：

  1. 通过多个 pass 可以实现在具有非常大 H 的情况下，还可以将随机访问的 $H_x$ 数量保持在很低的水平。更具体地说，就是如果我们能保证 $H_x = 2^{B_x}$ 同时小于 cache lines 的数量和 TLB entries 的数量，那么我们就可以在每个pass的分区中完全避免 TLB miss 和 cache miss。
  2. 在基于某列（一般是 join-key cloumn）的 $B$ bits 进行 radix-clustering 之后，该列的hash值中具有相同 $B$ bits 的所有 tuples 表现出连续性，通常会形成每 $C/2^B$ tuples 为一组的 chunks，其中 C 是输入的基数（cardinality）。因此，就没有必要使用额外的数据结构来记录这些 cluster 的边界：只需查看这些 clusters 的低 $B$ bits，就可以确定每个 cluster 的边界，这样就引入任何额外的开销。
  3. 此外，这种 radix-cluster 算法得到的输出还是基于 radix-bits 排序的。

图-9 中：

  • 在第一个 pass 中，取最左侧 2 bits 来划分，能得到 $4 = 2^2$ 个 clusters；
  • 在第二个 pass 中，此时取从最左侧开始的 $3^{th}$ bit，对第一个 pass 输出的每个 cluster 再进子行划分，此时总共得到 $8 = 2^1 * 4$ 个 clusters

对输出的 clusters 进行观察可得：

  • 有界性：即不需要额外的数据结构就可以确定每个 cluster 的边界。比如，我们可以观察最终输出数组中的hash值的低 $B=3$ bits 就能确定 {57, 17, 81, 75} 属于一个 cluster，而 96 和他们不是一个 cluster，并且这四个数字仍然保持原始输入中的顺序；
  • 有序性：最终输出的8个cluster是基于 3bits 进行排序的，即按照 000 --> 001 -->... --> 111 顺序递增

Experimental

radix-cluster 算法有三个参数会对性能造成影响，${B, P, B_p}$，论文进行试验，保持其中一个参数不变，变化另外两个参数对算法进行量化分析。

radix-bits

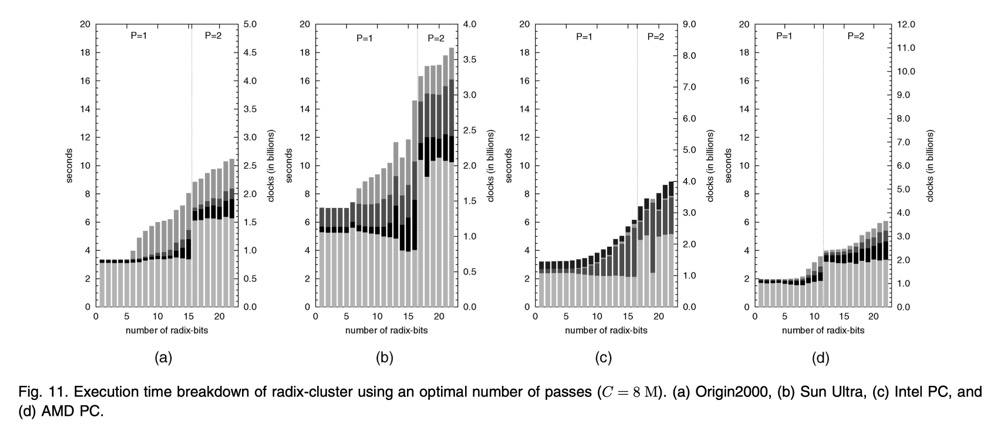
图-10展示了不同 CPU 架构下 1-pass 时不同 radix-bits 时执行时间分布细节。结论：

  • 纯CPU消耗的时间基本是恒定的，具体的数值在不同CPU架构上略有不同；
  • radix-bits 越小， memory 和 TLB 耗时越低，两者成正相关，即 radix-bits 增加，相应的耗时也会增加，比如当 radix-bits 超过 6 时，生成的 clusters 则超过了 TLB entries 的数量（$64 = 2^6）$，此时造成的 TLB miss 次数增加了，对应的耗时也会激增。cache miss 也类似。

不同 CPU 的 TLB entries 和 cache lines 数量都不一样，所以图 10 显示的 radix-bits 影响不同；

radix-join-3

multi-pass

图-11 展示了不同 passs 数量的影响。multipass radix-cluster 的核心思想是以增加 CPU 耗时来保证每个pass生成的 clusters 数量比较低，并降低内存耗。从图-11可得：

  • 在 radix-bits > 6 时，即便通过 2-pass 设计，CPU 的耗时成本过高以至于无法避免 TLB 的耗时；
  • 只有当 radix-bits > 15 时，即 内存耗时超过 CPU 耗时，2-passes 才超过 1-pass

    by the way，关于这两点的原文不知道是我理解错了，还是原文写错了，似乎结论和图-11不匹配，且这两点就互相矛盾。原文如下：

    • Obviously, the CPU costs are too high to avoid the TLB costs by using two passes with more than 6 radix-bits.
    • Only with more than 15 radix-bits (i.e., when the memory costs exceed the CPU costs) will two passes win over one pass

radix-join-4

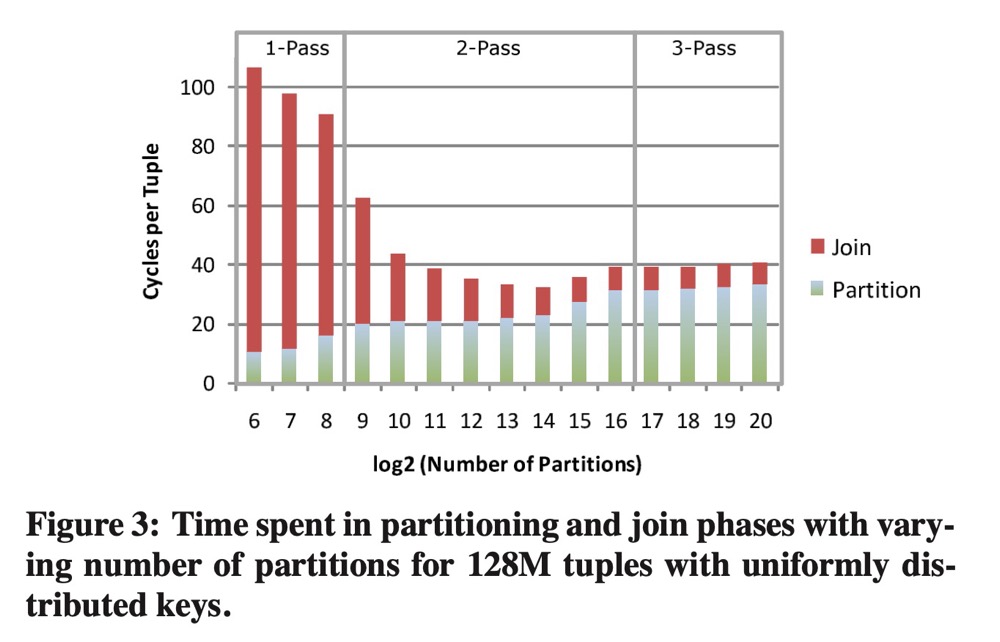
注意：图-11 展示的仅是分区这一个操作的耗时，当分区数据增多这个耗时不可避免的增加，但是分区 + join 操作的总体耗时不一定会增加，甚至可能会锐减。这里引用论文[3]中的一个分区和join操作总体耗时的图，更能说明问题。

radix-join-4-1

论文认为唯一改善图-11中问题的方法是降低 CPU 开销，图12是论文 1-pass 的 radix-cluster 算法源码，multi-pass 也是类似，所做的一个优化（图-12中的右侧两行代码）就是去掉了两个函数调用：

  • 将 hashFcn 变成宏；
  • 将 memcpy 替换为复制操作

radix-join-5

如图-13所示，优化之后，CPU 开销几乎降低了接近4倍，论文给出的两个理由是：

  • some CPU cycles are saved;
  • the CPUs can benefit more from the internal parallel capabilities using speculative execution as the code has become simpler and parallelization options more predictable

radix-join-6

Reference

  1. Optimizing Main-Memory Join on Modern Hardware
  2. Cache Conscious Algorithms for Relational Query Processing
  3. Sort vs. Hash Revisited: Fast Join Implementation on Modern Multi-Core CPUs