Hardware Memory Models

Sequential Consistency

文献[2]中首次提出顺序一致性 （Sequential Consistency），内容如下：

The customary approach to designing and proving the correctness of multiprocess algorithms for such a computer assumes that the following condition is satisfied:

• the result of any execution is the same as if the operations of all the processors were executed in some sequential order,
• and the operations of each individual processor appear in this sequence in the order specified by its program.

A multiprocessor satisfying this condition will be called sequentially consistent.

下面从 demo 开始说明 Sequential Consistency 及 Intel/ARM 架构下的内存模型。

Message Passing

Litmus Test: Message Passing
Can this program see r1 = 1, r2 = 0?
// Thread 1           // Thread 2
x = 1                 r1 = y
y = 1                 r2 = x

所有变量初始化为 0

如果编译器不 reorder 代码，在 Sequential Consistency 模型下的执行的结果，有如下六种可能：

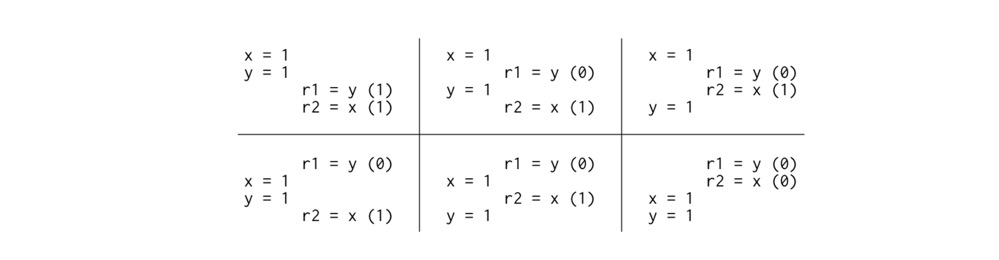
由于没有交叉执行，因此结果中没有 {r1 = 1, r2 = 0} 组合。也就是说，在 sequential consistency 硬件上，不可能看到 {r1= 1, r2 = 0} 的组合。

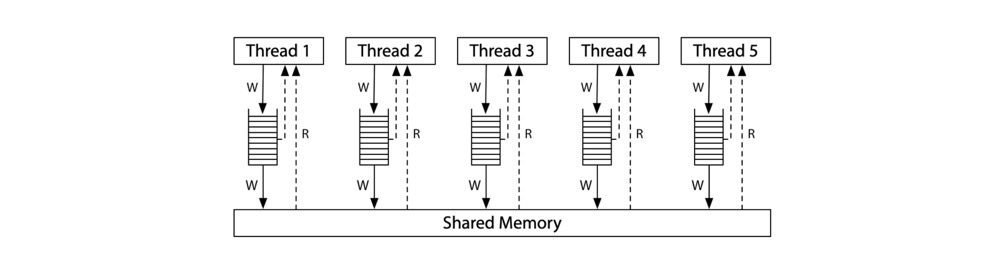
实现顺序一致性的内存模型可以成想象如下：所有的处理器都直接和共享内存（Shared Memory）连接，该共享内存一次只能为一个线程的读或者写请求服务。由于不涉及 cache，因此每次处理器需要读/写内存时，该请求都会经过共享内存。

这样就对所有访问内存的线程强加了一个顺序：Sequential Consistency。

此图只是顺序一致性机器的模型，而不是构建顺序一致性机器的唯一方法

然而，Sequential Consistency 内存模型会使得代码执行得非常慢，放弃严格的 Sequential Consistency 可以让硬件更快地执行程序，因此所有现代硬件都以各种方式偏离了 Sequential Consistency。

下面以 X86 和 ARM 架构为例。

X86: Total Store Order

现代 X86 架构内存模型如下：

所有处理器都仍然连接到单个 shared memory，但是每个处理器斗鱼一个 local wrire queue（又名 Write Store Buffer），即每个处理写时先写入 Write Store Buffer。处理器会继续执行新的指令，Write Store Buffer 按照 FIFO 规则进入 shared memory。一次 memory read 操作，会先尝试从自己 Write Store Buffer 中读取，如果没有则再从 shared memory 中读取。每个处理都看不到其他处理器的 Write Store Buffer。

引入 Write Store Buffer 后的影响就是：每个处理器都会比其他处理器先看见自己的写操作结果，但是所有的处理器有一点共识: 到达 shared memory 的写操作顺序对于所有的处理器来说都是一样的，并给这种模型取名为 Total Store Order，简称 TSO。

这段原文如下：The effect is that a processor sees its own writes before others do. But all processors do agree on the (total) order in which writes (stores) reach the shared memory, giving the model its name: total store order, or TSO。

因此，当写操作到达 shared memory 时，将来在任何处理器上的任何读操作都将看到它并使用该值（除非被后续的写操作覆盖）。

由于 Write Store Buffer 是个 FIFO 数据结构，因此一个处理器上的写操作不会乱序（即进入 shared memory，被其他处理器看见的顺序不会改变），并且只要 Write Store Buffer 中的写操作进入 shared memory，其他处理器就能立即看到，因此上述 Litmus Test 结果在 TSO 模型下还是不会出现 {r1 = 1, r2 = 0} 的结果

Litmus Test: Message Passing
Can this program see r1 = 1, r2 = 0?

// Thread 1           // Thread 2
x = 1                 r1 = y
y = 1                 r2 = x
On sequentially consistent hardware: no.
On x86 (or other TSO): no.

在 X86 内存模型中：

• Write Store Buffer 保证了线程 T1 中 x = 1 在 y = 1 之前先写入 shared memory，
• TSO 协议保证了线程 T2 会先看到 x 的新值，再看到 y 的新值

因此，线程 T2 不可能没有看到 x 的新值（r2 = 0），却看到了 y 的新值（r1 = 1）的情况。这里的 TSO 至关重要：线程 T1 先写 x 再写 y，TSO 保证了线程 T2 必须先看到 x 再看到 y。

Write Queue

Sequential Consistency 和 TSO 模型在上述 Litmus Test 中达到共识，但是下面的案例却并没有达成共识。

Litmus Test: Write Queue 
Can this program see r1 = 0, r2 = 0?

// Thread 1           // Thread 2
x = 1                 y = 1
r1 = y                r2 = x
On sequentially consistent hardware: no.
On x86 (or other TSO): yes!

在 Sequential Consistency 模型中，x = 1 和 y = 1 无论哪个先执行，一个线程在读取时都能看到另一个线程的更改，因此 {r1 = 0, r2 = 0} 不可能发生。但是在 TSO 模型中，T1 和 T2 分别将 x = 1 和 y = 1 缓存到各自的 Write Store Buffer，并在将 Write Store Buffer 同步到共享内存前，另一个线程就读取了 x or y，那么就有可能出现 {r1 = 0, r2 = 0} 的结果。原因简而言之，一个线程看不见另一个线程的写操作。

barriar

但是有些算法的正确性需要依赖更强 memory order，因此 non-sequentially-consistent 硬件提供了 memory barriers（or fences）指令，来显示控制 memory order。这样我们就可以添加一个 memory barrier，以确保每个线程在开始读之前先将它之前的写操作从 write store buffer 刷新到 shared memory 中。

// Thread 1           // Thread 2
x = 1                 y = 1
barrier               barrier
r1 = y                r2 = x

增加了 barriers 后，{r1 = 0, r2 = 0} 的情况也不可能发生。因此，barriers 给程序员和编译器提供了一个方法，在关键时刻强制保证代码按照 sequentially consistent 行为执行。

这里就对应 C++ 中的 std::memory_order_acquire 和 std::memory_order_release 语义

Why Total Store Order?

最后一个案例，来说明为什么 X86 内存模型叫做 Total Store Order。在 TSO 模型中，每个核只有一个 Write Store Buffer 用于缓存写操作，但是没有 Read Store Buffer 之类的设计。只要一个写操作进入了 shared memory，所有处理器就达成了2个共识：

1. 所有的 cpu 都能读取到该值

2. 变量(x)相对其他变量(y)到达 shared memory 的时间关系

   如果 x 比 y 先刷新到 shared memory，那么所有处理器都是先看到 x 再看到 y

比如下面的 demo 中，线程 T3 和 T4 有可能会以不同的顺序看到 {x, y} 吗？

Litmus Test: Independent Reads of Independent Writes (IRIW)
Can this program see r1 = 1, r2 = 0, r3 = 1, r4 = 0?
(Can Threads 3 and 4 see x and y change in different orders?)

// Thread 1    // Thread 2    // Thread 3    // Thread 4
x = 1          y = 1          r1 = x         r3 = y
                              r2 = y         r4 = x
On sequentially consistent hardware: no.
On x86 (or other TSO): no.

在 sequentially consistent 和 TSO 模型中都不可能。这就是 Total Store Order。这里的 store 即 write to shared memory。

所以 TSO 优化的是读路径: 有时可以从自己的 Write Store Buffer 读取，只有需要从其他线程读取共享变量时，才需要经过 shared memory。

ARM: Relaxed Memory Model

在内存一致性上，ARM 架构比 X86-TSO 提供的保证要弱得多。如图 ARM 的内存模型，特点如下：

• 每个处理器都有一个完整的内存副本，他们都分别读、写自己的内存副本，
• 每个写操作都独立地传播到其他处理器，并且在写操作传播时允许 reorder
• 每个处理器还允许将读操作延迟到它需要结果的时候，即 a read can be delayed until after a later write

在 ARM 架构下，由于没有 Total Store Order 保证，那么写指令传播过程中可能会发生 reorder，因此上述的 Litmus Tests 能全部能通过。

delay read

那么额外看下，ARM 架构下的延迟读问题，如下 demo：

Litmus Test: Load Buffering
Can this program see r1 = 1, r2 = 1?
(Can each thread's read happen after the other thread's write?)

// Thread 1    // Thread 2
r1 = x         r2 = y
y = 1          x = 1
On sequentially consistent hardware: no.
On x86 (or other TSO): no.
On ARM/POWER: yes!

在 sequentially consistent 模型下，r1 和 r2 至少有一个是 0。在 ARM 架构下，处理器是允许将读操作延迟到另一个线程对改变量的写操作之后，因此是有可能发生 y = 1 和 x = 1 先执行，再执行 r1 = x 和 r2 = y，即出现 {r1 = 1, r2 = 1} 的结果。

读也有了 buffer，当上下两条指令没有依赖，会被 reorder，导致 T1 的读操作延迟到 T2 的写操作之后

与 X86-TSO 系统类似，ARM 架构 也有 barrier 来强制某段代码具有 sequentially consistent。

Coherence

那么默认情况下，ARM 架构下的内存模型是什么也保证不了吗？下面来看看单个内存位置的并发写行为。

Litmus Test: Coherence
Can this program see r1 = 1, r2 = 2, r3 = 2, r4 = 1?
(Can Thread 3 see x = 1 before x = 2 while Thread 4 sees the reverse?)

// Thread 1    // Thread 2    // Thread 3    // Thread 4
x = 1          x = 2          r1 = x         r3 = x
                              r2 = x         r4 = x
On sequentially consistent hardware: no.
On x86 (or other TSO): no.
On ARM/POWER: no.

这个 demo 和 TSO 的最后一个 demo 很类似，区别是此处两个线程 T1、T2 写的是同一个变量 x，而不是两个不同的变量 x、y。那么线程 T3、T4 可能会看到变量 x 相反的赋值结果吗？答案是否定的。

即使在 ARM 架构上，系统中的线程必须就写入单个内存位置的总顺序达成一致，就像上述 demo，如果线程 T3 先看到的是 x = 1，再看到 x = 2，那么线程 T4 看到的顺序肯定也是一致的（如果没有看到 x = 1，r3 = r4 = 2 也是符合的），这就叫 coherence。如果没有 coherence，那么编码会变得非常困难。

Data-Race-Free

Adve and Hill 提出了一种同步模型（synchronization model），叫 Data-Race-Free（DRF），这个模型认为硬件应该提供内存同步操作（synchronization operations），这样可以普通的内存读写（Ordinary memory reads and writes）操作分割开来：普通的内存读写操作是可以在同步操作之间重新排序（reorder），但是不能跨过这些同步操作。也就说，这些同步操作也充当着 barriar 的角色，控制着 reorder 的边界。

一个程序如果被定义为 DRF 程序：

A program is said to be data-race-free if, for all idealized sequentially consistent executions, any two ordinary memory accesses to the same location from different threads are either both reads or else separated by synchronization operations forcing one to happen before the other

demo

下面的 demo-1 中，在单线程中对变量 x 进行先写后读操作，此时是没有竞争的。

下面这个 demo-2 中就存在竞争

线程 T2 对变量 x 的写操作并没有和线程 T1 协调好一个具体的时机。那么 T2 的写操作和 T1 中的写、读操作就都产生了竞争。如果 T2 中只是读操作，那么就只与 T1 中的写产生竞争：因为产生竞争至少需要一个写操作。

为了避免竞争，就必须添加同步操作，强制让不同线程操作共享变量时具有一个顺序性。如图，同步操作 $S(a)$ 表示对变量 a 施加同步操作(下图中的虚线表示)，强制让 T2 的写操作在 T1 完成后才发生（T2 happen after T1），那么竞争也消除了。

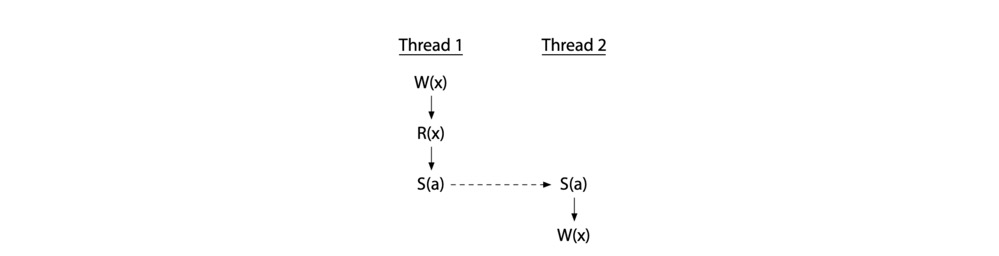
如果 T2 只有读操作，那么只需要同 T1 的写操作同步即可，两个线程对同一个变量进行读是可以并发的。

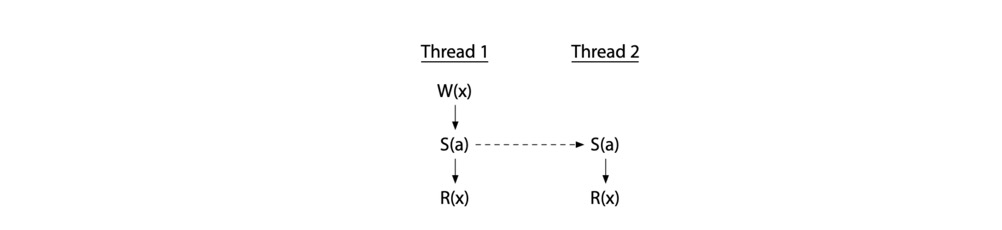
甚至可以添加中间同步变量，在多个线程间施加顺序，也是没有竞争。

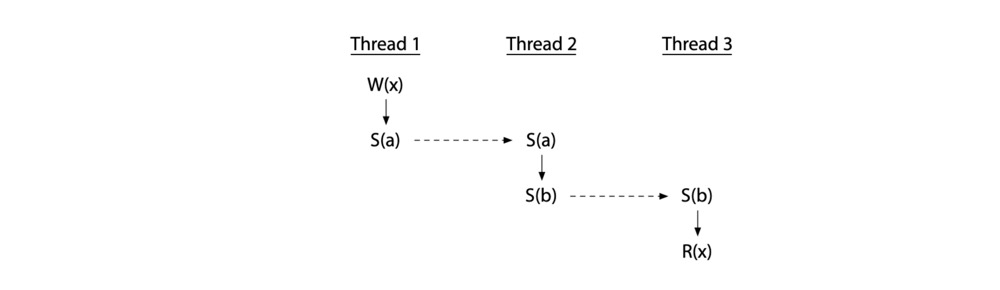
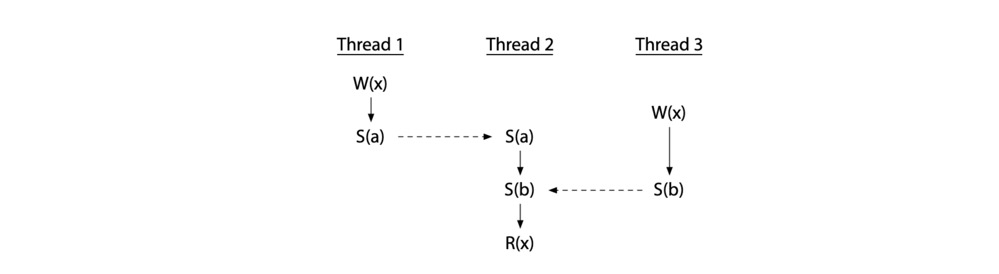
但是，并不是说使用了同步变量就一定不存在竞争了，错误使用还是会引入竞争。如图，T2 的读操作发生在在 T1、T3 的写操作之后，但是 T1 和 T3 的两个写操作之间并没有 happen before 的关系，因此还是存在竞争的，即不是 data-race-free 程序。

DRF-SC

Adve and Hill presented weak ordering as “a contract between software and hardware,” specifically that if software avoids data races, then hardware acts as if it is sequentially consistent, which is easier to reason about than the models we were examining in the earlier sections. But how can hardware satisfy its end of the contract?

Adve and Hill gave a proof that hardware “is weakly ordered by DRF,” meaning it executes data-race-free programs as if by a sequentially consistent ordering, provided it meets a set of certain minimum requirements. I’m not going to go through the details, but the point is that after the Adve and Hill paper, hardware designers had a cookbook recipe backed by a proof: do these things, and you can assert that your hardware will appear sequentially consistent to data-race-free programs. And in fact, most relaxed hardware did behave this way and has continued to do so, assuming appropriate implementations of the synchronization operations. Adve and Hill were concerned originally with the VAX, but certainly x86, ARM, and POWER can satisfy these constraints too. This idea that a system guarantees to data-race-free programs the appearance of sequential consistency is often abbreviated DRF-SC.

DRF-SC marked a turning point in hardware memory models, providing a clear strategy for both hardware designers and software authors, at least those writing software in assembly language. As we will see in the next post, the question of a memory model for a higher-level programming language does not have as neat and tidy an answer.

Reference

• [1] Hardware Memory Models
• [2] How to Make a Multiprocessor Computer That Correctly Executes Multiprocess Programs
• [3] Weak Ordering - A New Definition